Kryha Cryptanalysis - Find the structure of the wheel
Kryha Home Page
Kryha Cryptanalysis Home Page
- Wheel unknown, This page.
- Superposition Method
- Friedmand's Method
- Start sector
- Cryptograms in-depth
- Hill Climbing
Introduction
In kryha cryptanlysis, the most common situation is that we know nothing: the wheel used, the inner and outer alphabets, and the initial shifts.
Two methods are known:
- General Sacco's method
- Dr. Konheim's method
The rest of this page presents these two methods as well as my method which corresponds to a mix of the above methods and Friedman's method when the structure of the wheel has been found.
Regardless of the method used, the analysis is simpler if the number of sectors used is known. If this is not the case, it is necessary to proceed by trial and error or use the superposition method.
I describe the study of Dr. Konheim's cryptogram on another page.
General Sacco's Method
The Principle
In general, Sacco's method consists of dividing the letters of the cryptogram into 26 sets, each corresponding to an alphabet. Then, we try to solve the substitutions that form the basis of the different alphabets. Finally, we try to deduce pieces of plaintext.
Details of the Method
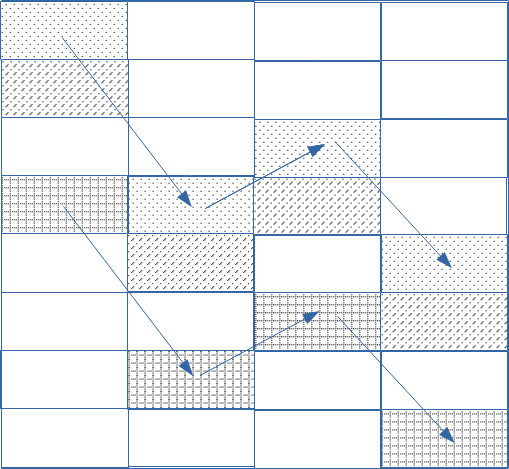
Figure: Only 4 columns (4 sectors) and 8 rows (normally 26 [as many as there are alphabets]) are shown. Cells with the same pattern belong to the same alphabet. If two cells belong to the same alphabet and are in two adjacent columns, the offset between the two cells will be the same for any other pair of cells in the same two columns.
1 - Creating a large table, each cell contains an alphabet
We distribute the cryptogram letter by letter into the cells of a table where each cell contains letters belonging to the same alphabet. This table has 26 rows corresponding to the 26 possible alphabets (the internal alphabet shifted in all possible ways), and as many columns as there are sectors of the wheel.
Note that, as a prerequisite, we must know the number of sectors of the wheel. The superposition method can provide this information. We can also try the dozen possibilities.
We observe that:
- a) Each cell contains letters belonging to the same alphabet.
- b) Each column will contain the same vertical sequence of cipher alphabets, but this sequence will be offset from adjacent sequences by an unknown number of cells.
- c) All 26 cipher alphabets of the machine will be present in each column, one per cell.
2 - Finding relations between cells
We begin by determining the position of at least one alphabet in each column. To do this, we will compare the contents of two cells belonging to two adjacent columns. We can use the index of coincidence calculated on all the letters in the two cells.
Finally, we will determine the alphabet used in each cell. If we cannot determine this, it will be a good indication that the assumed number of sectors is incorrect.
3 - Grouping alphabets in 26 sets
We will compile the letters from all the cells into a table containing the 26 alphabets.
4 - For each alphabet, we will try to deduce the most frequent letters
5 - We try do decipher part of the cryptogram
5 - We try do decipher part of the cryptogram
We apply our deductions to try to decipher part of the cryptogram. We will try to use probable words.
Example
Make a cryptogram
Let's take a very simple example in which we only use four sector. Structure of the wheel: 3,2,5,1.
$ cat MSGS/nightingale.raw
My heart aches, and a drowsy numbness pains
My sense, as though of hemlock I had drunk,
Or emptied some dull opiate to the drains
One minute past, and Lethe-wards had sunk:
'Tis not through envy of thy happy lot,
But being too happy in thine happiness,—
That thou, light-winged Dryad of the trees
In some melodious plot
Of beechen green, and shadows numberless,
Singest of summer in full-throated ease.
O, for a draught of vintage! that hath been
Cool'd a long age in the deep-delved earth,
Tasting of Flora and the country green,
Dance, and Provençal song, and sunburnt mirth!
O for a beaker full of the warm South,
Full of the true, the blushful Hippocrene,
With beaded bubbles winking at the brim,
And purple-stained mouth;
That I might drink, and leave the world unseen,
And with thee fade away into the forest dim:
Fade far away, dissolve, and quite forget
What thou among the leaves hast never known,
The weariness, the fever, and the fret
Here, where men sit and hear each other groan;
Where palsy shakes a few, sad, last gray hairs,
Where youth grows pale, and spectre-thin, and dies;
Where but to think is to be full of sorrow
And leaden-eyed despairs,
Where Beauty cannot keep her lustrous eyes,
Or new Love pine at them beyond to-morrow.
Away! away! for I will fly to thee,
Not charioted by Bacchus and his pards,
But on the viewless wings of Poesy,
Though the dull brain perplexes and retards:
Already with thee! tender is the night,
And haply the Queen-Moon is on her throne,
Cluster'd around by all her starry Fays;
But here there is no light,
Save what from heaven is with the breezes blown
Through verdurous glooms and winding mossy ways.
I cannot see what flowers are at my feet,
Nor what soft incense hangs upon the boughs,
But, in embalmed darkness, guess each sweet
Wherewith the seasonable month endows
The grass, the thicket, and the fruit-tree wild;
White hawthorn, and the pastoral eglantine;
Fast fading violets cover'd up in leaves;
And mid-May's eldest child,
The coming musk-rose, full of dewy wine,
The murmurous haunt of flies on summer eves.
Darkling I listen; and, for many a time
I have been half in love with easeful Death,
Call'd him soft names in many a mused rhyme,
To take into the air my quiet breath;
Now more than ever seems it rich to die,
To cease upon the midnight with no pain,
While thou art pouring forth thy soul abroad
In such an ecstasy!
Still wouldst thou sing, and I have ears in vain—
To thy high requiem become a sod.
Thou wast not born for death, immortal Bird!
No hungry generations tread thee down;
The voice I hear this passing night was heard
In ancient days by emperor and clown:
Perhaps the self-same song that found a path
Through the sad heart of Ruth, when, sick for home,
She stood in tears amid the alien corn;
The same that oft-times hath
Charm'd magic casements, opening on the foam
Of perilous seas, in faery lands forlorn.
Forlorn! the very word is like a bell
To toll me back from thee to my sole self!
Adieu! the fancy cannot cheat so well
As she is fam'd to do, deceiving elf.
Adieu! adieu! thy plaintive anthem fades
Past the near meadows, over the still stream,
Up the hill-side; and now 'tis buried deep
In the next valley-glades:
Was it a vision, or a waking dream?
Fled is that music:—Do I wake or sleep?
$ python3 kryha_tui.py -o -s 3,2,5,1 \
-i KPFQVGMASCHYNIORDELUBZWJXT \
-e ZCJBWYKNAGQSPFTROXVMDULEHI \
< MSGS/nightingale.raw >| /tmp/night.cry
$ python groupe.py < /tmp/night.cry
UFUIJ PXIGT WGPJS EFBUF STTSG NOTNC STRBW THIJF GOJZJ VBBAU
CPYAP TLKQE RWMPZ XSFYA IVWZV JUAHS YGVKT DHLKQ HWJLK BDSTY
LUWSJ DBJHK AENNI FKHHM WQKFG CNXHE PIWGF GRXLW UDXHH NXSMI
WVOSA NLSDR OVUSG EAZCK KQVMM PSREN VZPQN HDPPS HGEWH ULLKG
HARFM VGHXY TRWZA TXDVF IMPJM FEIBE QNUBJ ZXEUI MAHWK INEHG
GJNQP KWLKJ FAGHH MEQRW MJHOS EOZIK MVDYH ZPXYW JBDYU NYNFA
OEJUL ARPPD BXBBQ PNFJZ UCUCP YJAWZ DDWPM ZZMZK CNBTV YOQFC
PYHIC LGWYS MVDIB XMKWW BVYYS TQJXV HMOTL LUTMG HFPAT UYSGI
MIHCJ TCYYX KPSGI ZSVWI JUVEU EEEKX HBXNN MVOQS UNFES NRDGP
CWLLR QJOJD MZEBB ECPPS GAHOD QACKG UXJLY GVCAZ BZWHL NEAVR
PIURD OTBJG EBQDZ YTMCX SELHL AISKX HXLJB SROYN YLRDP SKHSL
SNGTA QDDSB POCQT PLJNU PFNQA NKIEA DZLRI JJUQH ITSVC DOLOH
ZWMPH SGIWO PMZFT BCPYC UNOMT VCMQH ALBDW GAHIF ZIJZH FAZDE
NWKCA ANGSO NWHDU GNJTZ IWNTE WPXMU JADSX JKGQT XVIRP CLLUA
WOEVB LTSHO WDWNZ JMYTS AARCX GXXRG FHQHA LUXIL DGYIM FLZDE
TXYJR CZWUT GHUAQ LOUEM XTTOY QWLSY TLVOA HZKJY JRUKG AQNNU
ZZORA PLJIK BSPJI DJGSW GIEIK VQBAG OSBSA IDKTF LTXPP JSQAF
OFZEA HRVZD ENBDJ UHEUL QLANY MTURR IHCLZ EFTTA ERXYE VKJXA
AKRKZ YQJOU JNWMJ CVSGK SQUGV DKBYR NJTJW WYBKI KFTNP GZHYI
KSRFY NYLRM RMNLS LHACQ KZZMS TFWJO EYERI BJICM ZTAII MRYCO
WEFBQ ARPXV TQVTF DRCVR YALEE KTDWX IKEAA UTMQU TBTNN JZCQS
SGCQK TGDSN ZHIWH JGTZU LIUFU GNOJH MINPM ENMLH DFZTF OHZNR
TSEYG ETHUR ITAOT JOZGQ NSDQN XNPTC YDUKA YBDPA SGIBD IFRKF
EQPDI LSMZM CPXCY EAABX JJSLT WXCAV FEYCF MVRWO CHPDA NHTGE
KWNRD TUJFF HBCQX QAYQS ICCGA CMNZJ GLQUN WGLKB TSOCY GEVWI
TJQHT ZTHJN DGSVJ ZXCMD SQGBR CZFZX HNLRX LYMTZ JRBGG AGFCF
XAGAK AYGIV DVZOC YLKVV RBFJI QHVLC ELODY AEWOG ORTZV KKJMB
WSOZL UGAUQ RVBSL JYFYI TEBON ZPROT NCGNI XWQIQ XMXON XIVPO
ZTLFY XMKIW GQAZB HFKBN FMOSE PZVHH LNJKE ROOWD MINCI PDGQI
GHSZZ WTYCG NCOVK ZQLLV YADCE WICTZ UQZKX HVFVQ KOPTC EFXQC
DQEAC CMWAC RNBXI OOFJS WZXYR IFHEQ FSEUG JZGFQ JUMXQ NCFVR
DXBLI MTMQF DDBJX GGDHD RGDQC GVZDL BXJEY DVDTZ RNGMM ZZJYU
FNWXT UEZJL VVBZQ WZWNR CYJPO LALBT THMMD OWQFW SXTUW SGXKQ
NPVQK GODBC SRVCW HBJYF FFSKI LDXTM ZKTLB FMYIE QXZWZ HPQXB
NHULG DWQEI CAEDV YATMS ZWYSG WLVGH RNCDI UCWXG CEUNF OXPYO
WKSUM XWPDZ VKOVS JEXJD MRQPC MFRRO LIFTC FYCBR VQUJG TBJDX
RWCBC POUPA PLSIS JJEDF YKQYE ICSNQ YORDE YCDVC RLZZZ VJVVU
QQHYU BDJBG SRDGA XFKHV FGDLE HKKXQ BWHUK TWDFV PMRER ZPBMC
UMZXV QTVHK TVLMN BVGPL PLBVM ADOLU YDACD REESN CZMKE BZRUU
FQNHF JURNP OLNJP YLZEK KPDEQ SJNQV OFEDL DWFIV NMGTU FVSDH
VTMQX JBOXF TVVIN QGFOE LIQSW CJWXS GYEUW TTZIM QHRDQ JPORV
XNWYH VWLQG TDFKV NFMRD IYBDF CAZEC UBMMW ZXQNR NHOJS EBIEW
YLAQA LGDTZ ATHYS OBDDS CNQSI VPMCB BBKKJ PLLBQ RYJZW UZZFM
IUTLI UXDSI YUGQK ATCAW PMVRH DUARB TXURO WOIKH LUFFJ FSCSF
DOFTX FQHGM ODNOS OJNLR ZCOUE VGLFW EYZHL HQGUO TASEX PBVZS
JVFNP XKWPD OQAGQ ATUHO WDHNF IYBEE ZVIYE GOVJU EVGKK PKBWJ
PEBWJ ZWNZE RPFFN IEBUF ICXOT PJDSR NJEIG VTQKZ QXCPT AYQAL
CQFYN AURRW JRXBI NOGSS HPFLJ KPNCZ RXPBE PYYSQ BTGCE XOUXV
WXAPA OYFZI JZSMK XKJGT SZVMC HUKZM YYNOV XAQRI JERTP TGYZB
CMRYH MFTNZ RRXLV OZVIZ GLCKS PJBZD VOBWG PCBIA CBAVQ MCUQH
NJOIR KIFYR TSXNU IGXKU YDDWD ZVHQC SKVIO UFGSG BGGUO BJWUA
XLIZB RQ
Create the big table (26xSectors)
My program chi2.py tries to distribute the letters of the cryptogram into an array Sectors x 26. It then tries to match the letters in one column with the letters in the next column.
The prerequisite is knowing the number of sectors on the wheel. You can, of course, try all possible values (less than 20) in turn, or use the superposition method.
]$ python3 chi2.py -c /tmp/night.cry -m 4 0: UJXBSSTRBYTDWOTDWJDJUOJGC,FDYBVEVGSBBIIZYDHDLNBWUCU, UBTQWLCFAKTFTLCBBMEQMOEEQ,IJRPIHMHIINRJUGJJRHVMIVXH, 1: JHWNJLQQDKNKQGNXYQKOWKGON,PKZFUAHHKFJFHACGFPKFZHKUJ, XAAJVIAATTZETUOGFCXEXLKXO,IETZESLLFNCQZQVDFMQDQUPVI, 2: GNXUUKBULPQPTRKHSFBLNFKWR,TNDCEXDXTGSDHVZDKRWDRFBXK, WIVUEHWIXZSIJBQRIRHWNJWAI,GFFCEXGLPHGLNSLGLOUFHFJPF, 3: PKIPKLADPYCSDLLDDLKIOSPAY,JHMYXJHGJIQMGJVQXITVJCEOR, SHPJHBIYSKKZSYYCTFWNSSBYT,EMJABSFIQSTMVFAGMTDMEFWFS, 4: FWMWXRZMARGCJYDVZCFGBDJZX,BQFZNOIFFFDPZICZKFVTIOZIN, UKEDNYJLOYSXXTEDTYPUEFWJU,FFIDMNZZFNNCCEWLLCMFWTNZI, 5: SGBWVYHDZYZYMBIBBBRVYXZSG,TCEPOLFEELHEDOCXFRESLFEMX, TNQMQRATARIASNTJMVRDAQRKK,SXNZSDZXHMWAQZZEYQZHQHPXU, 6: GHUZUPDYRRHBGPUYIUPVAGFKY,NEBMNSEJVMJXBRQDEJBTLMFJD, OPJZFKNRZNGJROZVQGMMGONGD,TIZKEHWCDLTJCTKDXTCQDDITW, 7: NWXCSSKZESZSZNXTZBUXTNESD,CGENNLCWNLULFCHZWJMJZOBZZ, SFUBRSAUBHLTZGVRZDZBASUVV,TGITDNATDAIWXNFNHXXOTOFMH, 8: RRMVGGNGJCUXHIVGPRVXHJICQ,BXAYPTGHUQFCNXQMQWQFYNCHC, WLHOCASUHKUALWKMXCTTSLXUS,TWWQWQOAEZGVRQOZBBVVOROKK, 9: HUKFLDNQUZNFXIPZNCHVBZTZV,IDICLDWLLMOELQTJHPKIDCPMI, JXNPRSHOQSJYYXCYUOTNDOJYO,FHEYQBDULTHCMMEULUVQSUDYU, 10: GHHHJPUEAFMFTXFFGPLGCESNF,ONGIOOGMNWIMZOXNDAMFNVROG, JXGCJCNXYJNVJNQWWPNOQGNVS,ZSJLDQJTMOPRRXCXQLBESLJXG, 11: JMNGMTTTTEMWBIDTESVLIFEAB,VIQWZPZOUYEOGVQUIIGIVWIQG, BWPYELIYRENCGPEECSPQPEGRG,BVKSBJWQRRMHAOAZAJLSMYVIU, 12: AOWMBNNWIILPGZCJEJPWCZTJO,USLVEUTLHBHDFTCLDELCBHQEB, CAKDCPESCJDACLMVVDBJBLKRJ,PNJIPFWYLIFNFFWVYFVWBHZTW, 13: YLFBPNPTZCZHXYABAYMXKQQPU,ASAXSQXLEMTTAXCZTKASKGXTA, PDGMGAMVFZFGGMRQMQDGJUCGX,TRHKANUOTTOEAKNWSYOYPOPYL, 14: LOHWHKJATAHKKIBZZELELTTZI,KVMWOIAHAIZWAWXWWIUULAABZ, QUEBDEDZEINNYGINYCYWBSYCB,ESQVQASKRMRRGQORSSDTQEQMR, 15: RGRYADXJXRTDIAOCGNATRXARQ,WEWYCZJYYYSTVZFYWQCZYPLY, MAMSKLKJECEUDBJJLYDIJBCH,PZJTGRGRVOYJVHSPVORMZVQM, 16: ZCHQUIQUKWGFZFWOGREQWZFF,XKOJXJTKJEEFOKZLHDEHUSYT, SKSXJJXGXFTHCBXARESRZJNN,FQEVLUVAABHBYNYLNYNDZVAZ, 17: YVOHYQIQAQUCLFRBCCCQFFUR,AMZMGHRNKARQKMITDDZJMNRR, IMIOVIPNRRIXVOFTIVMPIPRX,VPKTCTCUKPTQVSHHUCKOUXWL, 18: WSMLASLZZXAAREEMCRERTKJV,ZRVLZVLZYVOYBPQMWLBVLWRO, VEDUBCUOQTTQFZFDXZZXIPXZ,JNYTZDARJQJSJVSOGZRNUDBV, 19: UVHMWOWAOVOIIHEWCZUWXOII,AZZGHLOPUTZCQHUQEVUYDQNZ, HPPHLOELJFGCHLGFUJFHSAOG,SQXFNHVJNDQGVNJWNVQVIGGL, 20: YNYPEZBIWRNALJZSFVNWYQSC,GHWAAWLKMCSCCKGXOUHLUASK, VDJTVMTBJVDMEEFTXQFQGTHS,KPBURPSSCRQNLRQUPQJGQUPP, 21: TPDYPHHPVYNZOOJWYHUTKHFJ,DSYSISOJSAXJDOUSOYRDAOLB, HHUGUGWIGLNGYWMGWUNFTWJZ,LGNIRIDDKEPLADXXKBPKCDKD, 22: KEYMDWWJSETQEMQKSDOVAHPV,QWNIOONGQKCUWINQUJLNWNNO, HHFHTPZSUTYNONCNMBNFPFCB,WUACBMJWGDDWGCFPXGJMMIZW, 23: JLOJJZMGVWUGOIVVWSPRVYRG,LLETGFYIDXKLRPRQPRYDRBXP, KKJCETTEKIAKTDDKDDLIHEPC,BGUYBBSIBKYBZGXGZGZYDEBB, 24: DHLYQCAKYEBTVQBOVAEBUZEI,SAAXDPAVRADSKILDKXKDAVPA, TRRKZYRQNAPOKGIBOFKFRIYC,YFPPYCCBJUACJHMCVKPCBYYB, 25: LMPSTUXATTSYMSTSSHDATESA,UVDGMNGGJMGGBZMRJVEZXGQV, WGBICOXOWQIEWZQVEFQEUOBQ,SHXZXMXSWUBVSWFCXGSCRVTM, ...
Finding relations between cells
My program chi2.py, after distributing the letters of the cryptogram across a large array, attempts to match the alphabets in one column with the alphabets in the next column.
It considers pairs of alphabets. These pairs consist of the letters from one cell and the letters from another cell in the following column, shifted by a certain number of rows. If these two cells belong to the same alphabet, the IC (Index of Coincidences) of the letters in both cells is close to the IC characteristic of the language.
Since all cells in the same column have the same shift relative to the cells in the previous column, it is possible to calculate an IC that averages the 26 ICs corresponding to the 26 alphabets. This calculation is repeated for each pair of columns.
Here the result for our example (also created by the chi2.py program):
0 1 2 3
0: 0.035 0.038 0.029 0.040
1: 0.034 0.030 0.038 0.041
2: 0.048 0.035 0.044 0.035
3: 0.039 0.047 0.037 0.034
4: 0.027 0.031 0.037 0.042
5: 0.033 0.028 0.039 0.039
6: 0.048 0.042 0.040 0.037
7: 0.032 0.048 0.037 0.040
8: 0.029 0.035 0.039 0.067
9: 0.039 0.035 0.066 0.039
10: 0.043 0.040 0.042 0.034
11: 0.031 0.037 0.033 0.038
12: 0.031 0.035 0.040 0.042
13: 0.043 0.038 0.040 0.034
14: 0.044 0.068 0.036 0.038
15: 0.035 0.038 0.037 0.045
16: 0.033 0.031 0.043 0.042
17: 0.046 0.038 0.042 0.032
18: 0.039 0.042 0.029 0.032
19: 0.033 0.034 0.026 0.046
20: 0.041 0.039 0.043 0.037
21: 0.065 0.044 0.036 0.030
22: 0.032 0.042 0.034 0.032
23: 0.032 0.027 0.034 0.045
24: 0.044 0.026 0.046 0.032
25: 0.042 0.046 0.033 0.028
$
Here are the shifts found: 21, 14, 9, 8. They correspond to the maximum IC.
These shifts are relative. The absolute shifts are: 21, (21+14)%26==9, (9+9)==18, (18+8)%26==0, In short: 0, 21, 9, 18.
The cells that make up the different alphabets (column, row).
- 1st alphabet: (0,0),(1,21),(2,9),(3,18)
- 2nd alphabet: (0,1),(2,22),(2,10),(3,19)
- ...
- 26th alphabet: (0,25),(1,20),(2,8),(3,17)
For each alphabet, we will try to deduce the most frequent letters
I wrote another program that provides the characteristics of the 26 alphabets corresponding to the merging of the different cells in the different columns. The offsets for each column in the first alphabet are given as arguments.
$ python3 sacco_alpha.py -c /tmp/night.cry -m 0,21,9,18 0, 0.065 J:13,O:11,S:11,D:9,Y:8, 1, 0.082 N:19,Q:12,J:9,G:8,W:8, 2, 0.060 P:14,R:11,L:7,Q:7,E:6, 3, 0.078 D:16,K:12,A:11,L:9,P:9, 4, 0.071 G:17,M:12,D:7,J:7,Z:7, 5, 0.080 B:19,Y:13,G:8,Z:8,D:7, 6, 0.055 C:8,H:8,J:8,K:8,P:8, 7, 0.062 X:14,S:13,Z:7,D:6,N:6, 8, 0.075 I:15,J:11,R:10,V:10,H:8, 9, 0.062 Z:14,F:11,I:8,Q:8,D:6, 10, 0.078 F:16,L:11,E:10,G:10,H:10, 11, 0.066 M:12,T:12,E:10,F:8,J:8, 12, 0.061 N:11,W:11,Z:10,C:8,G:7, 13, 0.053 H:9,Q:9,N:8,Z:8,P:7, 14, 0.070 T:12,D:11,K:11,I:10,L:9, 15, 0.057 O:10,R:10,N:9,A:8,G:7, 16, 0.068 Q:13,W:11,O:10,I:8,Z:8, 17, 0.061 Q:10,U:10,C:9,L:9,B:8, 18, 0.060 A:12,X:12,T:9,E:7,L:7, 19, 0.066 W:14,I:13,A:10,H:6,O:6, 20, 0.066 Y:16,W:10,F:8,S:8,Z:7, 21, 0.055 Y:10,O:9,T:9,E:7,H:7, 22, 0.065 R:13,Q:11,M:10,A:8,K:7, 23, 0.064 V:13,G:9,O:9,R:9,Z:9, 24, 0.053 Z:10,V:9,A:8,B:8,U:8, 25, 0.066 S:12,T:10,U:9,A:8,C:8,
Note: It is observed that Sacco's method can find the 26 alphabets but not the shifts associated with each sector of the key. Therefore, it is not possible to use Friedman's method to reconstruct the alphabets and ultimately the plaintext.
We try do decipher part of the cryptogram
We apply our deductions to try to decipher part of the cryptogram. We will try to use probable words.
Note: You need to be a seasoned cryptologist to find the solution.
Konheim's Method
Konheim's method is mathematically very complex, and I confess I haven't fully grasped it… except for the beginning, which is quite usable as a complement to Sacco's method.
Consider two letters of the cryptogram, cry[i] and cry[j], where i and j correspond to the positions of the letters in the cryptogram.
The two letters belong to the same alphabet if and only if:
s * L = L[c1] – L[c2]
- L corresponds to the sum of the shifts of each sector. In the case of the standard wheel, L = 111.
- s corresponds to the number of periods, i.e., the difference in position between the two letters divided by the number of sectors.
- c1 corresponds to the index of the first letter modulo the number of sectors.
- c2, likewise, but for the second letter.
- L[x] = is the sum of the shifts of the sectors up to position x. = l[0] + l[1] + … + l[x]
- l[i] corresponds to the shift caused by the i-th sector.
Let's take an example with the standard wheel.
Consider the sequence of shifts for each sector.
[7, 6, 7, 5, 6, 7, 6, 8, 6, 10, 5, 6, 5, 7, 6, 5, 9] (l[0]=7, l[1]=6, l[2]=7, …, l[16]=9)If we look at the sequence of shifts for the first 30 characters:
0, 7, 13, 20, 25, 5, 12, 18, 0, 6, 16, 21, 1, 6, 13, 19, 24, 7, 14, 20, 1, 6, 12, 19, 25, 7, 13, 23, 2, 8,
We observe that the letters in positions 0 and 8 have the same shifts and therefore belong to the same alphabet. Similarly, the letters in positions 1 and 17, as well as the letters in positions 2 and 14, and the letters in positions 2 and 26.
Applying the formula to the last example, we have:
s = (26-2) // 17 = 1 L = 111 % 26 = 7 c1 = 2 % 17 = 2 c2 = 26 % 17 = 9 L[c1] = L[2] = 7 + 6 = 13 L[c2] = L[9] = 7 + 6 + 5 + 6 + 7 + 6 + 8 + 6 = 6 1 * 7 = 13 – 6 = 7
A Mixed Method
The difficulty with the Konheim method is that the parameters s, c1, and c2 are derived from complex statistical tables. In contrast, finding these parameters in the Sacco method is very simple. We constructed a table of Sectors x 26 cells, each cell containing the letters of the same alphabet. The coordinates of a cell were ci, ri (column, row). Using the Sacco method, we determined that some cells belong to the same alphabet.
s x L = L[c1] - L[c2] s = r2 – r1 (if c1 > c2)In our example, we thus have:
The cells (0,0) and (1,21) belong to the same alphabet, therefore we have:
21*L = L[0] – L[1]; L[0] == 0, L[1] = x1, that is, the shift associated with the first sector.
In total, we have (among others) the following equations:
21*L = 0 – x1 => 21*L + x1 = 0 14*L = 0 - x2 => 14*L + x2 = 0 9*L = 0 – x3 => 9*L + x3 = 0 7*L = 0 - x4 => 7*L + x4 = 0This system of equations allows us to find the unknowns: L, x1, x2, x3, x4.
We try all possible values of L (L=0 is impossible, because otherwise, all the cells in the first column would be encrypted with the same alphabet).
$ cat toto.py
for L in range(1,26):
x1 = (26 - (21*L)) % 26
x2 = (26 - (14*L)) % 26
x3 = (26 - ( 9*L)) % 26
x4 = (26 - ( 7*L)) % 26
diff = L - (x1+x2+x3+x4)
print("%2d : %2d %2d %2d %2d - %2d" % (L,x1,x2,x3,x4,diff))
$ python3 toto.py
1 : 5 12 17 19 - -52
2 : 10 24 8 12 - -52
3 : 15 10 25 5 - -52
4 : 20 22 16 24 - -78
5 : 25 8 7 17 - -52
6 : 4 20 24 10 - -52
7 : 9 6 15 3 - -26
8 : 14 18 6 22 - -52
9 : 19 4 23 15 - -52
10 : 24 16 14 8 - -52
11 : 3 2 5 1 - 0
12 : 8 14 22 20 - -52
13 : 13 0 13 13 - -26
14 : 18 12 4 6 - -26
15 : 23 24 21 25 - -78
16 : 2 10 12 18 - -26
17 : 7 22 3 11 - -26
18 : 12 8 20 4 - -26
19 : 17 20 11 23 - -52
20 : 22 6 2 16 - -26
21 : 1 18 19 9 - -26
22 : 6 4 10 2 - 0
23 : 11 16 1 21 - -26
24 : 16 2 18 14 - -26
25 : 21 14 9 7 - -26
The only possible outcome is: x1=3, x2=2, x3=5, x4=1, and L=11
.
From this, we can calculate all the offsets associated with each cell:
0: 0 3 5 10 1: 11 14 16 21 2: 22 25 1 6 3: 7 10 12 17 4: 18 21 23 2 5: 3 6 8 13 6: 14 17 19 24 7: 25 2 4 9 8: 10 13 15 20 9: 21 24 0 5 10: 6 9 11 16 11: 17 20 22 1 12: 2 5 7 12 13: 13 16 18 23 14: 24 1 3 8 15: 9 12 14 19 16: 20 23 25 4 17: 5 8 10 15 18: 16 19 21 0 19: 1 4 6 11 20: 12 15 17 22 21: 23 0 2 7 22: 8 11 13 18 23: 19 22 24 3 24: 4 7 9 14 25: 15 18 20 25 26: 0 3 5 10 27: 11 14 16 21 28: 22 25 1 6 29: 7 10 12 17We can verify that the cells (0,0) and (1,21) do indeed belong to the same alphabet!
Friedman's method
Now that we know the wheel, we can use Friedman's method:
$ python3 friedman_start.py -c /tmp/night.cry -w 3,2,5,1
Wheel: [3, 2, 5, 1] Sector: 0
1: 0.065306
2: 0.045301
3: 0.046654
4: 0.044419
$ python3 friedman_end.py -c /tmp/night.cry -w 3,2,5,1
A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
0: 3 4 2 9 0 0 2 1 1 13 0 1 0 4 11 1 2 5 11 5 5 2 2 4 8 2
1:10 4 1 0 2 0 0 6 13 4 2 2 4 1 6 0 2 4 3 0 6 6 14 3 1 5
2: 1 2 8 1 3 6 7 3 5 6 0 7 5 11 3 2 0 0 0 3 4 0 11 0 1 10
3: 0 19 3 7 5 1 8 2 6 0 1 1 1 4 0 0 1 1 5 0 4 4 3 2 13 8
4: 8 8 2 4 5 2 2 5 1 0 1 5 0 4 2 1 6 2 3 3 8 9 0 0 6 10
5: 2 8 9 4 8 7 0 6 1 0 1 9 4 0 2 0 10 2 2 6 10 3 1 0 4 0
6: 2 0 5 1 10 16 10 10 0 4 0 11 2 2 5 7 0 1 4 2 3 0 0 4 0 0
7:11 3 6 16 2 0 1 0 5 3 12 9 1 1 1 9 0 3 5 0 0 4 0 4 2 0
8: 8 0 0 6 5 0 2 2 2 3 7 0 10 4 2 1 11 13 7 6 0 4 2 0 1 2
9: 8 1 2 5 0 5 7 2 7 1 3 0 4 9 10 1 2 10 0 7 0 1 2 7 3 2
10: 0 0 3 0 1 1 7 8 15 11 0 0 7 3 3 5 3 10 0 2 2 10 0 7 1 0
11: 0 0 3 2 0 1 8 2 3 9 5 3 0 19 6 1 12 0 2 0 2 6 8 4 2 0
12: 1 4 4 0 2 8 0 3 4 4 2 3 0 6 0 5 2 1 8 4 0 4 10 0 16 7
13: 4 5 6 1 1 6 1 9 0 0 1 1 4 8 1 7 9 0 3 4 4 0 2 7 7 8
14: 5 6 8 3 2 7 4 8 2 8 8 2 3 0 0 8 0 2 1 0 8 2 0 0 8 3
15: 8 0 8 1 1 0 2 7 0 0 8 7 4 0 3 3 1 0 12 10 9 2 5 5 1 0
16:12 1 4 1 7 1 3 0 1 5 4 7 4 0 3 1 3 5 7 9 1 2 1 12 0 5
17: 3 7 0 6 10 8 3 1 3 8 0 2 12 3 0 0 4 1 6 12 0 6 2 2 0 0
18: 3 3 5 7 1 5 17 0 1 7 0 0 12 1 0 2 3 4 0 0 3 5 6 5 1 7
19: 0 2 0 1 0 1 9 1 1 7 1 5 6 3 9 5 3 9 2 1 1 13 4 0 4 9
20: 1 4 2 0 6 5 7 1 8 0 3 0 0 0 10 1 13 3 0 1 5 7 11 1 1 8
21: 0 3 4 6 3 11 0 2 8 0 2 3 1 6 3 4 8 0 1 5 5 6 0 4 0 14
22: 0 5 3 2 6 3 6 1 2 1 5 7 0 4 0 14 7 11 4 2 6 0 2 3 4 0
23: 2 0 0 4 7 3 0 7 0 7 7 3 0 4 9 6 0 1 3 9 6 1 3 4 10 2
24: 3 1 7 11 7 0 0 6 10 4 11 9 2 0 2 3 2 0 0 12 0 0 4 1 0 4
25: 1 4 5 6 4 3 3 3 0 3 4 0 2 6 0 0 0 5 13 6 2 3 4 14 0 7
A: 3 10 1 0 8 2 2 11 8 8 0 0 1 4 5 8 12 3 3 0 1 0 0 2 3 1 : 96
B: 4 4 2 19 8 8 0 3 0 1 0 0 4 5 6 0 1 7 3 2 4 3 5 0 1 4 : 94
C: 2 1 8 3 2 9 5 6 0 2 3 3 4 6 8 8 4 0 5 0 2 4 3 0 7 5 :100
D: 9 0 1 7 4 4 1 16 6 5 0 2 0 1 3 1 1 6 7 1 0 6 2 4 11 6 :104
E: 0 2 3 5 5 8 10 2 5 0 1 0 2 1 2 1 7 10 1 0 6 3 6 7 7 4 : 98
F: 0 0 6 1 2 7 16 0 0 5 1 1 8 6 7 0 1 8 5 1 5 11 3 3 0 3 :100
G: 2 0 7 8 2 0 10 1 2 7 7 8 0 1 4 2 3 3 17 9 7 0 6 0 0 3 :109
H: 1 6 3 2 5 6 10 0 2 2 8 2 3 9 8 7 0 1 0 1 1 2 1 7 6 3 : 96
I: 1 13 5 6 1 1 0 5 2 7 15 3 4 0 2 0 1 3 1 1 8 8 2 0 10 0 : 99
J:13 4 6 0 0 0 4 3 3 1 11 9 4 0 8 0 5 8 7 7 0 0 1 7 4 3 :108
K: 0 2 0 1 1 1 0 12 7 3 0 5 2 1 8 8 4 0 0 1 3 2 5 7 11 4 : 88
L: 1 2 7 1 5 9 11 9 0 0 0 3 3 1 2 7 7 2 0 5 0 3 7 3 9 0 : 97
M: 0 4 5 1 0 4 2 1 10 4 7 0 0 4 3 4 4 12 12 6 0 1 0 0 2 2 : 88
N: 4 1 11 4 4 0 2 1 4 9 3 19 6 8 0 0 0 3 1 3 0 6 4 4 0 6 :103
O:11 6 3 0 2 2 5 1 2 10 3 6 0 1 0 3 3 0 0 9 10 3 0 9 2 0 : 91
P: 1 0 2 0 1 0 7 9 1 1 5 1 5 7 8 3 1 0 2 5 1 4 14 6 3 0 : 87
Q: 2 2 0 1 6 10 0 0 11 2 3 12 2 9 0 1 3 4 3 3 13 8 7 0 2 0 :104
R: 5 4 0 1 2 2 1 3 13 10 10 0 1 0 2 0 5 1 4 9 3 0 11 1 0 5 : 93
S:11 3 0 5 3 2 4 5 7 0 0 2 8 3 1 12 7 6 0 2 0 1 4 3 0 13 :102
T: 5 0 3 0 3 6 2 0 6 7 2 0 4 4 0 10 9 12 0 1 1 5 2 9 12 6 :109
U: 5 6 4 4 8 10 3 0 0 0 2 2 0 4 8 9 1 0 3 1 5 5 6 6 0 2 : 94
V: 2 6 0 4 9 3 0 4 4 1 10 6 4 0 2 2 2 6 5 13 7 6 0 1 0 3 :100
W: 2 14 11 3 0 1 0 0 2 2 0 8 10 2 0 5 1 2 6 4 11 0 2 3 4 4 : 97
X: 4 3 0 2 0 0 4 4 0 7 7 4 0 7 0 5 12 2 5 0 1 4 3 4 1 14 : 93
Y: 8 1 1 13 6 4 0 2 1 3 1 2 16 7 8 1 0 0 1 4 1 0 4 10 0 0 : 94
Z: 2 5 10 8 10 0 0 0 2 2 0 0 7 8 3 0 5 0 7 9 8 14 0 2 4 7 :113
25
[[25, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0],
[0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0],
[0, 0], [0, 0], [0, 0], [0, 0], [0, 0], [0, 0]]
[[25, 0], [19, 22], [6, 16], [9, 24], [16, 18], [3, 5], [13, 9], [18, 13], [21, 17],
[5, 19], [2, 12], [8, 8], [4, 4], [22, 25], [11, 3], [7, 11], [0, 14], [24, 10],
[20, 2], [1, 1], [23, 23], [17, 6], [14, 7], [12, 15], [10, 21], [15, 20]]
Z: 2 5 10 8 10 0 0 0 2 2 0 0 7 8 3 0 5 0 7 9 8 14 0 2 4 7 , 0
T: 2 9 12 6 5 0 3 0 3 6 2 0 6 7 2 0 4 4 0 10 9 12 0 1 1 5 ,22
G: 3 3 17 9 7 0 6 0 0 3 2 0 7 8 2 0 10 1 2 7 7 8 0 1 4 2 ,16
J: 4 3 13 4 6 0 0 0 4 3 3 1 11 9 4 0 8 0 5 8 7 7 0 0 1 7 ,24
Q: 3 3 13 8 7 0 2 0 2 2 0 1 6 10 0 0 11 2 3 12 2 9 0 1 3 4 ,18
D: 4 1 16 6 5 0 2 0 1 3 1 1 6 7 1 0 6 2 4 11 6 9 0 1 7 4 , 5
N: 9 3 19 6 8 0 0 0 3 1 3 0 6 4 4 0 6 4 1 11 4 4 0 2 1 4 , 9
S: 3 1 12 7 6 0 2 0 1 4 3 0 13 11 3 0 5 3 2 4 5 7 0 0 2 8 ,13
V: 6 5 13 7 6 0 1 0 3 2 6 0 4 9 3 0 4 4 1 10 6 4 0 2 2 2 ,17
F: 1 5 11 3 3 0 3 0 0 6 1 2 7 16 0 0 5 1 1 8 6 7 0 1 8 5 ,19
C: 4 6 8 8 4 0 5 0 2 4 3 0 7 5 2 1 8 3 2 9 5 6 0 2 3 3 ,12
I: 2 7 15 3 4 0 2 0 1 3 1 1 8 8 2 0 10 0 1 13 5 6 1 1 0 5 , 8
E: 5 8 10 2 5 0 1 0 2 1 2 1 7 10 1 0 6 3 6 7 7 4 0 2 3 5 , 4
W: 4 2 14 11 3 0 1 0 0 2 2 0 8 10 2 0 5 1 2 6 4 11 0 2 3 4 ,25
L: 1 5 9 11 9 0 0 0 3 3 1 2 7 7 2 0 5 0 3 7 3 9 0 1 2 7 , 3
H: 2 3 9 8 7 0 1 0 1 1 2 1 7 6 3 1 6 3 2 5 6 10 0 2 2 8 ,11
A: 5 8 12 3 3 0 1 0 0 2 3 1 3 10 1 0 8 2 2 11 8 8 0 0 1 4 ,14
Y: 1 2 16 7 8 1 0 0 1 4 1 0 4 10 0 0 8 1 1 13 6 4 0 2 1 3 ,10
U: 4 4 8 10 3 0 0 0 2 2 0 4 8 9 1 0 3 1 5 5 6 6 0 2 5 6 , 2
B: 4 2 19 8 8 0 3 0 1 0 0 4 5 6 0 1 7 3 2 4 3 5 0 1 4 4 , 1
X: 4 1 14 4 3 0 2 0 0 4 4 0 7 7 4 0 7 0 5 12 2 5 0 1 4 3 ,23
R: 1 3 13 10 10 0 1 0 2 0 5 1 4 9 3 0 11 1 0 5 5 4 0 1 2 2 , 6
O: 1 2 10 3 6 0 1 0 3 3 0 0 9 10 3 0 9 2 0 11 6 3 0 2 2 5 , 7
M: 4 4 12 12 6 0 1 0 0 2 2 0 4 5 1 0 4 2 1 10 4 7 0 0 4 3 ,15
K: 2 5 7 11 4 0 2 0 1 1 1 0 12 7 3 0 5 2 1 8 8 4 0 0 1 3 ,21
P: 1 4 14 6 3 0 1 0 2 0 1 0 7 9 1 1 5 1 5 7 8 3 1 0 2 5 ,20
Interior Alphabet: ZWJXTKPFQVGMASCHYNIORDELUB , Collision: False
$
$ python3 kryha_tui.py -o -i ZWJXTKPFQVGMASCHYNIORDELUB -d -s 3,2,5,1 \
< /tmp/night.cry >| /tmp/night_pseudo.txt
$ python ic.py /tmp/night_pseudo.txt
YKDCNUTNGDCQNMZNZUVJQKMAYIMCQQRNEMQYKQCMQCNQTDVAODVSDCYBVGLE...
0.065179326076
$ pypy2 hc_substi.py -c /tmp/night_pseudo.txt -t 3
(0, 17551.977587319026, 'GMINSOTSFINASEDSDORCAMELGBENAAYSHEAGMANEANSATIRLWI')
(1, 19208.78372139837, 'MYHEARTACHESANDADROWSYNUMBNESSPAINSMYSENSEASTHOUGH')
(2, 19208.78372139837, 'MYHEARTACHESANDADROWSYNUMBNESSPAINSMYSENSEASTHOUGH')
()
('Key: ', 'NIGZCSODEFLBYMVRPUQTAXJWKH', ' Score: ', 19208.78372139837)
MYHEARTACHESANDADROWSYNUMBNESSPAINSMYSENSEASTHOUGHOFHEMLOCKIHADDRUNKOREMPTI
EDSOMEDULLOPIATETOTHEDRAINSONEMINUTEPASTANDLETHEWARDSHADSUNKTISNOTTHROUGHEN
VYOFTHYHAPPYLOTBUTBEINGTOOHAPPYINTHINEHAPPINESSTHATTHOULIGHTWINGEDDRYADOFTH
ETREESINSOMEMELODIOUSPLOTOFBEECHENGREENANDSHADOWSNUMBERLESSSINGESTOFSUMMERI
NFULLTHROATEDEASEOFORADRAUGHTOFVINTAGETHATHATHBEENCOOLDALONGAGEINTHEDEEPDEL
VEDEARTHTASTINGOFFLORAANDTHECOUNTRYGREENDANCEANDPROVENALSONGANDSUNBURNTMIRT
HOFORABEAKERFULLOFTHEWARMSOUTHFULLOFTHETRUETHEBLUSHFULHIPPOCRENEWITHBEADEDB
UBBLESWINKINGATTHEBRIMANDPURPLESTAINEDMOUTHTHATIMIGHTDRINKANDLEAVETHEWORLDU
NSEENANDWITHTHEEFADEAWAYINTOTHEFORESTDIMFADEFARAWAYDISSOLVEANDQUITEFORGETWH
ATTHOUAMONGTHELEAVESHASTNEVERKNOWNTHEWEARINESSTHEFEVERANDTHEFRETHEREWHEREME
NSITANDHEAREACHOTHERGROANWHEREPALSYSHAKESAFEWSADLASTGRAYHAIRSWHEREYOUTHGROW
SPALEANDSPECTRETHINANDDIESWHEREBUTTOTHINKISTOBEFULLOFSORROWANDLEADENEYEDDES
PAIRSWHEREBEAUTYCANNOTKEEPHERLUSTROUSEYESORNEWLOVEPINEATTHEMBEYONDTOMORROWA
WAYAWAYFORIWILLFLYTOTHEENOTCHARIOTEDBYBACCHUSANDHISPARDSBUTONTHEVIEWLESSWIN
GSOFPOESYTHOUGHTHEDULLBRAINPERPLEXESANDRETARDSALREADYWITHTHEETENDERISTHENIG
HTANDHAPLYTHEQUEENMOONISONHERTHRONECLUSTERDAROUNDBYALLHERSTARRYFAYSBUTHERET
HEREISNOLIGHTSAVEWHATFROMHEAVENISWITHTHEBREEJESBLOWNTHROUGHVERDUROUSGLOOMSA
NDWINDINGMOSSYWAYSICANNOTSEEWHATFLOWERSAREATMYFEETNORWHATSOFTINCENSEHANGSUP
ONTHEBOUGHSBUTINEMBALMEDDARKNESSGUESSEACHSWEETWHEREWITHTHESEASONABLEMONTHEN
DOWSTHEGRASSTHETHICKETANDTHEFRUITTREEWILDWHITEHAWTHORNANDTHEPASTORALEGLANTI
NEFASTFADINGVIOLETSCOVERDUPINLEAVESANDMIDMAYSELDESTCHILDTHECOMINGMUSKROSEFU
LLOFDEWYWINETHEMURMUROUSHAUNTOFFLIESONSUMMEREVESDARKLINGILISTENANDFORMANYAT
IMEIHAVEBEENHALFINLOVEWITHEASEFULDEATHCALLDHIMSOFTNAMESINMANYAMUSEDRHYMETOT
AKEINTOTHEAIRMYQUIETBREATHNOWMORETHANEVERSEEMSITRICHTODIETOCEASEUPONTHEMIDN
IGHTWITHNOPAINWHILETHOUARTPOURINGFORTHTHYSOULABROADINSUCHANECSTASYSTILLWOUL
DSTTHOUSINGANDIHAVEEARSINVAINTOTHYHIGHREQUIEMBECOMEASODTHOUWASTNOTBORNFORDE
ATHIMMORTALBIRDNOHUNGRYGENERATIONSTREADTHEEDOWNTHEVOICEIHEARTHISPASSINGNIGH
TWASHEARDINANCIENTDAYSBYEMPERORANDCLOWNPERHAPSTHESELFSAMESONGTHATFOUNDAPATH
THROUGHTHESADHEARTOFRUTHWHENSICKFORHOMESHESTOODINTEARSAMIDTHEALIENCORNTHESA
METHATOFTTIMESHATHCHARMDMAGICCASEMENTSOPENINGONTHEFOAMOFPERILOUSSEASINFAERY
LANDSFORLORNFORLORNTHEVERYWORDISLIKEABELLTOTOLLMEBACKFROMTHEETOMYSOLESELFAD
IEUTHEFANCYCANNOTCHEATSOWELLASSHEISFAMDTODODECEIVINGELFADIEUADIEUTHYPLAINTI
VEANTHEMFADESPASTTHENEARMEADOWSOVERTHESTILLSTREAMUPTHEHILLSIDEANDNOWTISBURI
EDDEEPINTHENEXTVALLEYGLADESWASITAVISIONORAWAKINGDREAMFLEDISTHATMUSICDOIWAKE
ORSLEEP
$
References
Articles & Books
- Manuel de Cryptographie, Par le Général L. Sacco, (1951), Payot, Paris. French edition by Captain J. Brès based on the third Italian edition revised by the author.
- Cryptanlysis of a Kryha Machine, by A.G. Konheim. Article of a book: Lecture Notes in Computer Science, Edited by G. Goos and J. Hartmanis, 159, Cryptography, Proceeding, Burg Feuertein, (1982), Edited by Thomas Beth, Springer-Verlag, Berlin Heidelberg New York.